海量数据处理算法
基本方法
hash法
前言
适用于在处理海量数据的过程中,使用hash方法一般可以快速存取、统计某些数据,将大量数据进行分类,例如提取某日访问网站次数最多的ip地址。
简介
hash主要用来进行“快速存取”,在O(1)时间复杂度里就可以找到目标元素,或者判断是否存在。hash一般被称为散列,给定关键字key,按一个确定的散列函数计算出hash(key),把hash(key)作为关键字key对应元素的存储地址(或者称散列地址)。散列函数就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。散列函数是用于关键字与存储地址之间的一种映射关系。散列表是具有固定大小的数组,其中,表长(数组的大小)应该为质数。但是不能保证每个关键字与函数值一一对应,就是有可能存在冲突。所以确定一个好的散列函数至关重要。
常用散列函数的构建方法一般有以下几种:
(1) 直接寻址法
取关键字或关键字的某个线性函数值为散列地址,即h(key) = key 或 h(key)= a*key+b,其中a,b均为正整常数,这种散列函数叫做自身函数。散列函数取关键字自身,但是这种方法效率比较低,时间复杂度为O(1),空间复杂度O(n),n为关键字的个数。
直接寻址法不会产生冲突,但是由于没有压缩映像,因此集合很大时变得不切实际。
(2) 取模法
选择一个适合的正整数m,令h(key)=key mod m, m选择较大的素数比较好,一般是散列表的表长。
(3) 数值分析法
设关键字的d位的以r为基的数(例如以10为基的十进制数),且共有n个关键字,则关键字的每个位可能有r个不同的数符出现(即0,1,…,9),但这个r个数符在各个位上出现的频率不一定相同,选取其中各种符号分布均匀的的若干位作为散列地址。
例如:散列表地址范围有三位数,观察下列关键吗后,取各关键吗的4,5,6位作为记录的散列地址。
1 | 8 5 3 2 4 8 |
数值分析法仅适用于事先明确知道所有关键字的每一位的分布情况,所以使用局限。
(4)折叠法
将关键字分成位数有t的几部分(最后一部分的位数可能小于t),然后把各部分按位对齐相加,将所的和舍弃进位,留下t位作为散列地址。当关键字很多,而且关键字中每位上的数字分布比较均匀时,采用折叠法比较合适。
(5)平方取中法
这是一个较常用的方法,将关键字进行平方运算,然后从结果的中间取出若干位(位数与散列地址的位数相同),将其作为散列地址。
(6)除留余数法
这是一种比较常用的散列函数,其主要原理是取关键字除以某数m(m不大于散列表长度)的余数作为散列地址,即hash(key)=key % m,m一般是散列表的长度,并且时质数。
(7)随机数法
选择一个随机函数,然后用关键字key的随机函数值作为散列地址,即hash(key)=random(key),random()为随机函数。但关键字长度不相等时,采用这个方法适合。
在构造散列函数的过程,不管用什么散列函数总是会存在散列冲突问题,下面是几种解决散列冲突的方法:
(1)开放定址法
基本思想是当发生冲突时,在散列表中再按照某种中方法继续探测其他的存储地址,直到找到空闲的地址为止。
该过程可描述为
1 | hash_i(key) = (hash(key) +d(i)) mod m (i=1,2,...,k( k<=m-1 )) |
其中,hash(key)为关键字key的直接散列地址,m 为散列表的长度,d(i)为每次再探测时的地址增量。
增量d(i)可以有不同的取法,常用有以下三种:
a. d(i)=1,2,…,m-1, 称为线性探测法。
b. d(i)=1^2,-1^2,2^2,-2^2,…, 称为二次探测法。
c. d(i)=为伪随机序列,称为伪随机探测法。
下面举个例子来说明查找成功的平均查找长度(ASLsucc)和查找不成功的平均查找长度(ASLunsucc):
例题一:
关键字为{75,29,48,94,25,22,45},散列函数为hash(key)=key%23,采用线性探测法处理冲突。
1 | 地址号 0 1 2 3 4 5 6 7 ... 22 |
ASLsucc=(2+1+2+2+1+2+1)/7=1.59
ASLunsucc=(16+2+4+3+2+3+2+3)/23=1.52
(2)链接法
基本思想是通过链表数组来解决冲突(HashMap的数据结构),通过hash函数定位到固定长的数组下标,如有冲突则添加到相连的链表中。
(3)再散列法
当发生冲突时,使用第二个、第三个、第四个hash函数计算地址,直到没有冲突为止。这种方法的缺点是计算时间大幅度增加。
(4)建立一个公共溢出区
假设散列函数的值域为[0,m-1],则设向量HashTable[0…m-1]为基本表,另外设立存储空间向量OverTable[0…v]用于存储发生冲突的记录。
Bit-map法
前言
适用于海量数据的快速查找、判重、删除等。
简介
Bit-map(位图)法的基本原理是使用位数组来表示某些元素是否存在。具体而言,Bit-map法的结果是生成一个N位长的串,每位上以“1”或“0”表示需要排序的集合中的数。例如集合位{2,6,4,9,1,10},则生成一个10位的串,将2、6、4、9、1、10位置为“1”,其余是“0”,当把串中所有的位都置完后,排序也自动完成了,结果是11001001011。
Bit-map法排序的时间复杂度是O(n),比一般的排序都快,但它是以空间换时间的,而且有些限制,即数据状态不是很多,例如排序前集合的大小最好已知,而且集合中的元素的最大重复次数必须已知,最好是惆集数据(不然空间浪费很大)。
Bloom Filter法
前言
在海量数据处理中,经常需要判断一个元素是否在集合中,Bloom Filter法可以解决此问题。
简介
Bloom Filter法是一种空间效率和时间效率都很高的随机数据结构,可用来检测一个元素是否属于一个集合。但他同样带来了问题,牺牲了正确性。具体而言,查询结果俩种可能,即“不属于这个集合(绝对正确)”和“属于这个集合(可能错误)”。
基本原理是位数组和hash函数的联合使用。首先,Bloom Filter是包含了m位的位数组,数组的每一个位都是初始化为0,;其次,定义k个不同的hash函数,每个函数都可以集合中的元素映射到数组的某一位,将这些位置于“1”.如果查询某个元素是否属于集合,那么根据k个hash函数可以得到位数组的k位,查看k位,如果有的位不为“1”,则钙元素肯定不存在;如果全部为“1”,则可能存在。
Trie树
前言
Trie树的典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
简介
Trie 这个单词来自“retrieve”,Trie 树又称字典树或键树,它是一种用于快速字符串检索的多叉树结构,其原理是利用字符串的公共前缀来减少时空开销,即空间换时间。它的优点是:最大限制地减少无谓的字符串比较,查询效率比散列表高。缺点:若系统中存在大量字符串且这些字符串基本没有公共前缀,这对应的Trie树非常的消费内存。
Trie树的一般具有3个特性:
(1)根节点不包含字符,除根结点外每一个节点都只包含一个字符。
(2)从根节点到某一结点,路径上经过的字符串连起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符不相同。
例子:要保存5个字符串tea,ten,to,int,inn.如图所示: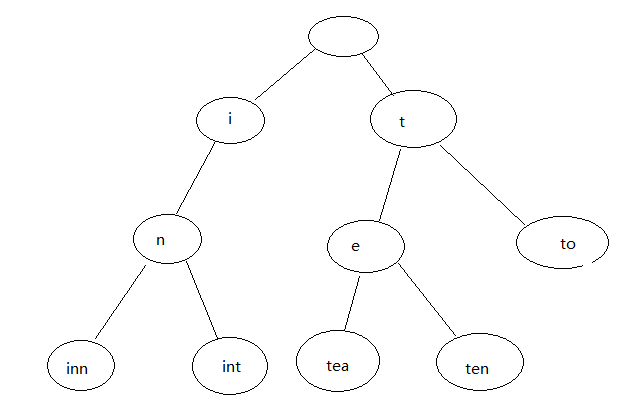
堆
前言
堆特别适合海量数据中寻找前N大数据(最大堆)或者前N小数据问题,其中N比较小。
简介
堆是一种树形结构,每个节点都有一个值,而通常所说的堆,一般是指二叉堆,有最大堆和最小堆。
双层桶法
前言
桶排序一般适用于寻找第K大的数、寻找中位数、寻找不重复或重复的数字等情况。
简介
双层桶不是数据结构,而是一种算法实现,类似于分治思想,其次并不是分两次,“双”只是个拟词,只要没达到要求就可以继续分。因为元素范围很大,不能利用直接寻址表,所以通过多次划分,逐步确定范围,然后最后在一个可以接受的范围内进行。桶排序的平均时间复杂度为O(n),最坏情况下O(n^2)。
例子:存在集合{11,2,5,17,45,31,36,27,26},用桶排序。
解题:
最大值为45,所以分成了5个桶,并在桶内进行选择/堆/快排后在整合在一起。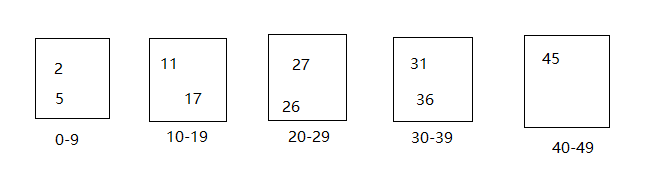
经典实例分析
top K问题
前言
在海量数据处理时经常遇到需要寻找出现频率最高的或最大的前K个数,这类问题通常被称为top K问题,例如搜索引擎中,统计搜索引擎的最热门10个查询词,或者最热门的20个歌曲。
简介
针对top K类问题,通常比较好的方案是分治+Trie树/hash+小顶堆,即先将数据集按照hash方法分解成多个小的数据集,然后使用Trie树或者hash统计每个小数据集中的查询词频之后用小顶堆求出每个数据集中出频率最高的前K个数,最后在所有top K中求出最终的top K。
例如,有1亿个浮点数,如何找出其中的最大的10000个?
第一种方法:将数据全部排序,然后在排序后的集合中查找,最快的排序算法的时间复杂度为O(nlogn),例如快排、归并。这个方法效率不高,不想讨论。
第二种方法:局部淘汰法,该方法于排序方法类似,用一个容器保存前10000个数,然后将剩余的数字跟容器内最小的数比较,如果大则替换,最后容器的10000数就是前10000个数了。此时的时间复杂度为O(n+m^2),m为容器大小,即10000.
第三种方法:分治法,将1亿数据分成100份,每份100万个数据,找出每份数据中最大的10000个,最后剩下100×10000数据找出最大的10000个。如果100万数据选的足够理想,那么可以过滤掉99%的数据。100万个数据里面查找最大的10000个数据的方法如下:用快速排序的方法,将数据分成两堆,如果大的那个堆个数N大于10000个,继续对大堆快速排序依次分成两堆;如果大堆个数n小于10000个,就在小的堆里面快排一次,找第10000-n大的数字;递归以上操作,就可以找到10000大的数了。此方法每次需要的内存空间为100万*4=4M,一共需要101次这样的比较。
第四种方法:hash法,如果这1亿个数据里面哟据很多的重复的数据,则通过hash方法去重,可以提高效率,然后再运用分治法或最小堆法进行查找最大的10000个数。
第五种方法:最小堆方法,先读入前10000个数字来创建小顶堆,建堆的时间为O(mlogm)(m为数组的大小),然后遍历其余数据,并于堆顶比较,若比堆顶小,则替换调整最小堆。遍历完数据按中序遍历输出10000个数。该算法的时间复杂度为O(nmlogm),空间复杂度为10000。
究竟采用哪种方法,按实际问题和实际应用场景而定,灵活运用。
下面针对不同的应用场景,分析了合适相应应用场景的解决方案。
(1)单机+单核+足够大的内存
内存够用的情况下,直接全部读取,顺序遍历查找top K即可。
(2)单机+多核+足够大的内存
这时可以直接再内存中使用hash方法将数据分成c*n个部分(c>1,n为处理器个数),每一部分都分给一个线程来执行,当一个线程完成时主动获取下一个部分,直至数据处理完毕,并用一个线程将结果归并。
(3)单机+单核+内存受限
这时需要将原数据文件割成一个一个小文件,如采用hash(x)% M,将文件分割成M个小文件,这样每个文件放到内存中既可以采用方法(1)一次处理每个小文件了。
(4)多机+内存受限
这是纪要把文件分发到多台设备来处理。
其实在现实中1-4的方法并不可行,因为在大规模的数据处理环境中,作业的效率并不是首要考虑的问题,算法的扩展性和容错性才是首要考虑的。所以top K问题很适用于MapReduce上解决。
下面是一些历年来经常被各大互联网公司提及的top K问题:
(1)搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。假设目前有一千万个记录,请你统计最热门的10个查询串,要求使用的内存不能超过1G。。
分析:
有1000万记录,去重后大概有300万记录,每个算255字节,因此把他们都装内存需要3M*1KB4=0.75GB,所以可以把所有记录在内存中处理,用HashMap在合适不过了。放弃分而治之方法。
解题:
第一步:先对这批海量数据预处理。具体方法是:维护一个Key为Query字串,Value为该Query出现次数的HashMap,即HashMap(Query,Value),每次读取一个Query,如果该字串不在Map中,那么加入该字串,并将Value值设为1;如果该字串在Map中,那么将该字串的计数加1即可。最终我们在O(N)的时间复杂度内用Hash表完成了统计。
第二步:可以维护k个元素的最小堆,即用容量为k的最小堆存储k个元素,每次堆顶比较,如果更小则替换并调整最小堆。总费时O(k*logk+(n-k)*logk)=O(n*logk)。
(2)提取某日访问网站次数最多的ip。
分析:
百度作为国内第一大搜索引擎,每天访问它的IP数量巨大,如果想一次性把所有IP数据装进内存处理,则内存容量明显不够,故针对数据太大,内存受限的情况,可以把大文件化成(取模映射)小文件,从而大而化小,逐个处理。换言之,先映射,而后统计,最后排序。
解题:
分而治之hash映射:首先把这一天访问百度的日志的所有IP提取出来,然后逐个写入到一个大文件中,接着采用映射的方法,比如%1000,把整个大文件映射为1000个小文件。
hash_map统计:当大文件转化了小文件,那么我们便可以采用hash_map(ip,value)来分别对1000个小文件中的IP进行频率统计,再找出每个小文件中出现频率最大的IP及相应的频率。
堆/快速排序:统计出1000个频率最大的IP后,进行排序(可采取堆排序),找出那个频率最大的IP,即为所求。
说明:
Hash取模是一种等价映射,不会存在同一个元素分散到不同小文件中去的情况,即这里采用的是%1000算法,那么同一个IP在hash后,只可能落在同一个文件中,不可能被分散的。
(3)有一个10文件,每个文件1GB,每个文件的每一行都存放的是用户的query,每个文件的query都可能重复。请按照query的频率排序。
解题:
hash映射:顺序读取10个文件,按照hash(query)%10的结果将query写入到另外10个文件(记为a0,a1,..a9)中。这样新生成的文件每个的大小大约也1G(假设hash函数是随机的)。
hash_map统计:找一台内存在2G左右的机器,依次对用hash_map(query, query_count)来统计每个query出现的次数。
注:hash_map(query,query_count)是用来统计每个query的出现次数,不是存储他们的值,出现一次,则count+1。
堆/快速/归并排序:利用快速/堆/归并排序按照出现次数进行排序,将排序好的query和对应的query_cout输出到文件中,这样得到了10个排好序的文件。最后,对这10个文件进行归并排序(内排序与外排序相结合)。
重复问题
前言
在海量数据中查找出重复出现的元素或者去除重复出现的元素也是常考的内容。例如,已知某文件包含一些电话号码,每个号码为8位数,统计不同的号码的个数。
简介
针对此类问题,一般用位图法实现。8位整数可以表示的最大进制数值为99999999,如果每个数字对应于位图中的1个bit位,那么存储8位正整数需要99Mbit,因为1byte=8bit,所以99Mbit折合成内存为99/8=12.375MB的内存,即用12.375MB来表示所有的8位电话号码的内容。
下面是一些历年来经常被各大互联网公司提及的重复问题:
(1)10亿个正整数,只有1个重复出现过,要求再O(n)的时间里找出这个数。
解题:
用位图法,10亿数据就需要用1Gbit空间,即125MB空间,不算多,并且能找到重复的数字。
(2)给定a,b两个文件,个存放50亿个url,每个url各占用64byte,要求再O(n)的时间里找出啊a、b文件共同的url。
分析:
50亿数据就是5*64GB=320GB大小,一般内存都装不下,所以需要分而治之法。
解题:
分而治之/hash映射:遍历文件a,对每个url求取hash(url)%1000,然后根据所取得的值将url分别存储到1000个小文件(记为a0,a1,..,a999)中。这样每个小文件的大约为300M。遍历文件b,采取和a相同的方式将url分别存储到1000小文件中(记为b0,b1,…,b999)。这样处理后,所有可能相同的url都在对应的小文件(a0vsb0,a1vsb1,…)中,不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
hash_set统计:求每对小文件中相同的url时,可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url,看其是否在刚才构建的hash_set中,如果是,那么就是共同的url,存到文件里面就可以了。
排序问题
前言
海量数据处理中类常见的问题就是排序。例如,9亿条不重复的9位整数,对这个文件中的数字进行排序。
简介
对于此类问题,最直接的方法是全部导入内存并排序,但是这个一般不可行,需要考虑其它的方法:
方法一,数据库排序法。将文本文件导入到数据库中,让数据库进行索引排序后在读取到文件中。该方法虽然操作简单、方便,但是运算慢,而且对数据库设备要求比较高。
方法二,分治法。通过hash法将9亿条数据分为20段,每段大约5000万条,大约占5000万*4B=200MB空间,在文件中一次搜索05000万,5001万1亿…将排序的结果存入文件。该方法需要遍历20次文件,虽然缩小了每次使用内存空间大小,但是编码复杂,速度慢。
方法三,位图法。由于9亿条数据,所以9Gbit空间,即大约120MB空间。如果存在某数字,则下标置为“1”,这样就排序完了。
下面是一些历年来经常被各大互联网公司提及的排序问题:
有关正整数的情况就是用位图法。